Imaginary Numbers (i): How “Fake” Numbers Have Real Power

Imaginary numbers emerged from mathematicians’ attempts to solve equations that seemed impossible within the realm of real numbers. The most fundamental imaginary number, denoted as i, is defined as the square root of -1. This definition might seem nonsensical at first—after all, any real number multiplied by itself gives a positive result, so how can a number squared equal -1? Yet this “impossible” concept opened up entirely new mathematical territories.

The equation x² + 1 = 0 is the simplest example of an unsolvable equation in real numbers. Rearranging it gives x² = -1, which has no real solution because no real number squared can equal a negative number. However, by introducing i such that i² = -1, we can write the solutions as x = ±i. This mathematical extension transforms an impossible problem into one with two clear solutions.

The historical development of imaginary numbers began with cubic equations in the 16th century. Mathematicians like Gerolamo Cardano and Rafael Bombelli encountered square roots of negative numbers while solving certain cubic equations, even when all solutions were real. These “imaginary” intermediate steps were necessary to arrive at real solutions, demonstrating that imaginary numbers, while seemingly nonsensical, had practical mathematical value.

Consider the cubic equation x³ = 15x + 4. Using Cardano’s formula, the solution involves the expression ∛(2 + √(-121)) + ∛(2 – √(-121)). At first glance, this seems problematic because of the square root of a negative number. However, Bombelli discovered that if we treat √(-121) as 11i, the expression simplifies to 2 + 11i and 2 – 11i. Remarkably, when these complex numbers are cube-rooted and added, the imaginary parts cancel out, yielding the real solution x = 4.

Quadratic equations provide another class of problems where imaginary numbers become essential. The quadratic formula x = [-b ± √(b² – 4ac)] / (2a) can yield imaginary results when the discriminant (b² – 4ac) is negative. For example, the equation x² + 2x + 5 = 0 has discriminant 4 – 20 = -16, so the solutions are x = [-2 ± √(-16)] / 2 = [-2 ± 4i] / 2 = -1 ± 2i. Without imaginary numbers, we would have to say this equation has no solutions, but with them, we find two complex solutions.

Higher-degree polynomial equations also benefit from the inclusion of imaginary numbers. The fundamental theorem of algebra states that every non-constant polynomial equation with complex coefficients has at least one complex root. This mathematical theorem guarantees that by extending our number system to include imaginary numbers, we ensure that all polynomial equations have solutions.

The mathematical concept of field extensions explains how imaginary numbers expand the real number system. The real numbers form a field, meaning we can add, subtract, multiply, and divide (except by zero) and always get real results. When we add i to the real numbers and close under arithmetic operations, we get the complex numbers, which also form a field. This mathematical structure preserves all the familiar algebraic properties while adding new capabilities.

Imaginary numbers also solve differential equations that model physical phenomena. For example, the differential equation d²y/dx² + y = 0 (which describes simple harmonic motion) has solutions involving sine and cosine functions. These solutions can be expressed more elegantly using complex exponentials: y = Ae^(ix) + Be^(-ix), where A and B are constants determined by initial conditions.

In electrical engineering, imaginary numbers are essential for analyzing alternating current (AC) circuits. The impedance of capacitors and inductors is represented as imaginary numbers, allowing engineers to use complex arithmetic to analyze circuit behavior. Without imaginary numbers, the mathematical analysis of AC circuits would be significantly more complicated.

Quantum mechanics provides perhaps the most profound application of imaginary numbers in fundamental physics. The Schrödinger equation, which describes how quantum systems evolve over time, involves the imaginary unit i: iℏ ∂ψ/∂t = Ĥψ. The wave function ψ is complex-valued, and the presence of i is essential for the equation’s ability to describe quantum phenomena accurately.

The mathematical beauty of imaginary numbers lies in how they complete the algebraic structure of numbers. With real numbers alone, we cannot solve all polynomial equations. With complex numbers (real numbers plus imaginary numbers), we can solve any polynomial equation, making the complex number system algebraically closed.

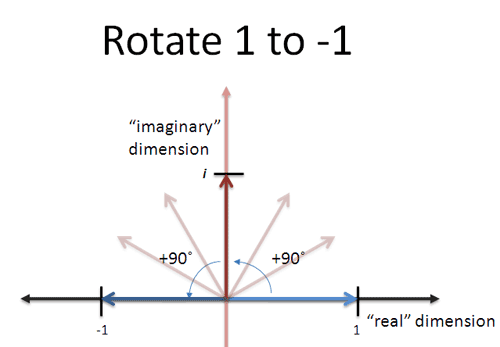
Imaginary numbers also enable the mathematical representation of rotations and oscillations. Multiplying a complex number by i corresponds to rotating it 90 degrees counterclockwise in the complex plane. This geometric interpretation connects algebraic operations with spatial transformations, providing powerful tools for mathematical analysis.

The complex plane is a geometric representation that makes imaginary and complex numbers visually intuitive. Also known as the Argand plane, named after Jean-Robert Argand who popularized its use, this two-dimensional coordinate system extends the familiar real number line into a plane where each point represents a complex number. The horizontal axis represents the real part, and the vertical axis represents the imaginary part.

Any complex number can be written in the form a + bi, where a and b are real numbers, and i is the imaginary unit with the property i² = -1. In the complex plane, this number corresponds to the point (a, b). For example, the complex number 3 + 4i is represented by the point (3, 4), three units to the right and four units up from the origin.

The origin (0, 0) in the complex plane represents the complex number 0 + 0i, or simply 0. The positive real axis (horizontal line to the right of the origin) represents positive real numbers, while the negative real axis represents negative real numbers. The positive imaginary axis (vertical line above the origin) represents positive imaginary numbers like i, 2i, 3i, etc., and the negative imaginary axis represents negative imaginary numbers like -i, -2i, -3i, etc.

The geometric interpretation of complex number addition follows vector addition. To add two complex numbers, we add their corresponding vectors tip-to-tail. For example, adding (3 + 4i) + (1 + 2i) corresponds to adding the vectors from the origin to (3, 4) and from (3, 4) to (4, 6), resulting in the complex number 4 + 6i represented by the point (4, 6).

Multiplication by i has a beautiful geometric interpretation: it corresponds to a 90-degree counterclockwise rotation about the origin. Multiplying 1 + 0i by i gives 0 + 1i, which rotates the point (1, 0) to (0, 1). Multiplying by i again gives i² = -1, rotating (0, 1) to (-1, 0). Another multiplication by i gives -i, rotating (-1, 0) to (0, -1), and a final multiplication returns to the original position: (-i) × i = -i² = -(-1) = 1.

The modulus (or absolute value) of a complex number a + bi is its distance from the origin in the complex plane: |a + bi| = √(a² + b²). This mathematical definition extends the concept of absolute value from real numbers to complex numbers. For example, the modulus of 3 + 4i is √(3² + 4²) = √(9 + 16) = √25 = 5. Geometrically, this is the length of the vector from the origin to the point (3, 4).

The argument (or phase) of a complex number is the angle it makes with the positive real axis, measured counterclockwise. For a complex number a + bi, the argument θ satisfies tan(θ) = b/a. The argument is usually expressed in radians and can be calculated using the arctangent function, with adjustments needed for different quadrants. For 3 + 4i, the argument is arctan(4/3) ≈ 0.93 radians or about 53.13 degrees.

Polar form represents complex numbers using their modulus and argument: z = r(cos θ + i sin θ), where r is the modulus and θ is the argument. This form is particularly useful for multiplication and division. When multiplying two complex numbers in polar form, we multiply their moduli and add their arguments: (r₁∠θ₁) × (r₂∠θ₂) = (r₁r₂)∠(θ₁ + θ₂).

Euler’s formula, e^(iθ) = cos θ + i sin θ, connects exponential functions with trigonometry and provides an elegant way to represent complex numbers in polar form: z = re^(iθ). This mathematical relationship simplifies many calculations involving complex numbers and reveals deep connections between exponential growth, periodic oscillations, and circular motion.

Complex conjugation reflects a complex number across the real axis. The complex conjugate of a + bi is a – bi, represented geometrically by reflecting the point (a, b) across the horizontal axis to (a, -b). Complex conjugates have the same modulus but opposite arguments, and their product is always a non-negative real number: (a + bi)(a – bi) = a² + b².

Roots of complex numbers have geometric interpretations in the complex plane. The nth roots of a complex number are equally spaced points on a circle centered at the origin. For example, the three cube roots of 1 are located at 120-degree intervals around the unit circle, at angles 0°, 120°, and 240°. This geometric pattern reflects the mathematical relationship between roots and rotations.

Transformations in the complex plane provide visual insights into complex functions. Linear functions like f(z) = az + b correspond to scaling, rotation, and translation. More complex functions like f(z) = z² or f(z) = e^z transform geometric shapes in predictable ways, creating beautiful fractal patterns and revealing the geometric nature of complex analysis.

The complex plane also enables visualization of complex-valued functions of a complex variable. Domain coloring techniques assign colors to points in the complex plane based on the function’s value at those points, creating stunning visual representations that reveal the behavior of complex functions in ways that would be impossible with real-valued functions alone.

Understanding the complex plane is essential for applications in physics and engineering. In electrical engineering, impedance is represented as complex numbers in the complex plane, with resistance on the real axis and reactance on the imaginary axis. In fluid dynamics, complex potentials describe fluid flow patterns. In signal processing, the frequency domain representation uses the complex plane to analyze signals.

Imaginary numbers, despite their name, have incredibly practical applications in the real world, particularly in electrical engineering and quantum mechanics. These “imaginary” mathematical constructs are essential tools for understanding and designing the technology that powers our modern world, from smartphones to quantum computers.

In electrical engineering, imaginary numbers are fundamental to analyzing alternating current (AC) circuits. Unlike direct current (DC), which flows in one direction, AC current oscillates sinusoidally, changing direction many times per second. The mathematical analysis of AC circuits involves complex numbers, where the real part represents resistive elements and the imaginary part represents reactive elements like capacitors and inductors.

Impedance is a complex quantity that generalizes resistance to AC circuits. For a resistor, impedance Z = R (purely real). For a capacitor, impedance Z = -i/(ωC), where ω is the angular frequency and C is capacitance. For an inductor, impedance Z = iωL, where L is inductance. The imaginary unit i captures the phase relationship between voltage and current in reactive components: capacitors cause current to lead voltage by 90 degrees, while inductors cause current to lag voltage by 90 degrees.

Phasor analysis uses complex numbers to simplify AC circuit calculations. A sinusoidal voltage V(t) = V₀cos(ωt + φ) can be represented as a complex phasor V = V₀e^(iφ), where the magnitude represents the peak voltage and the argument represents the phase angle. This mathematical representation converts differential equations describing circuit behavior into algebraic equations in the complex domain, making analysis much simpler.

In power systems, complex power S = P + iQ combines real power P (which does useful work) and reactive power Q (which supports electromagnetic fields but doesn’t do net work). The magnitude |S| is the apparent power, and the ratio P/|S| is the power factor, a crucial parameter for electrical efficiency. Utilities often charge penalties for poor power factors, making the mathematical understanding of complex power essential for economic operation.

Signal processing relies heavily on imaginary numbers through the Fourier transform, which decomposes signals into frequency components. The Fourier transform of a real signal is generally complex-valued, with the real part representing cosine components and the imaginary part representing sine components. This mathematical tool is essential for audio processing, image processing, data compression, and telecommunications.

Digital signal processors (DSPs) and many microcontrollers have specialized hardware for complex arithmetic to efficiently implement algorithms like the Fast Fourier Transform (FFT). These mathematical operations enable technologies like MP3 compression, digital radio, and mobile communications. Without imaginary numbers, the mathematical foundation for these technologies would be much more complicated.

In control systems engineering, the Laplace transform converts differential equations into algebraic equations in the complex frequency domain. The complex variable s = σ + iω represents both exponential decay/growth (σ) and oscillatory behavior (ω). The location of poles and zeros in the complex plane determines system stability and response characteristics, making complex analysis essential for designing stable control systems.

Quantum mechanics is perhaps the most profound application of imaginary numbers in fundamental physics. The wave function ψ(x, t), which contains all information about a quantum system, is generally complex-valued. The Schrödinger equation iℏ ∂ψ/∂t = Ĥψ explicitly involves the imaginary unit, and the presence of i is essential for the equation’s ability to describe quantum phenomena correctly.

The probability density in quantum mechanics is given by |ψ|² = ψ*ψ, where ψ* is the complex conjugate of ψ. This mathematical construction ensures that probability is real and non-negative, but it requires the wave function to be complex. The interference effects that are central to quantum mechanics—like those in the double-slit experiment—depend on the complex nature of the wave function.

Operators in quantum mechanics, which correspond to measurable quantities, often involve imaginary numbers. The momentum operator is -iℏ ∂/∂x, and the angular momentum operators involve combinations of position and derivative operators with imaginary coefficients. These mathematical constructs ensure that the operators have real eigenvalues, corresponding to physically measurable quantities.

In quantum field theory, which describes fundamental particles and forces, complex numbers are essential for describing particle creation and annihilation, gauge symmetries, and the mathematical structure of spacetime. The mathematical framework of quantum electrodynamics, which describes the electromagnetic force, relies on complex-valued fields and path integrals.

Modern technologies like lasers, MRI machines, computer processors, and quantum computers all depend on quantum mechanical principles that require imaginary numbers for their mathematical description. The quantum bits (qubits) in quantum computers exist in superposition states that are mathematically described using complex numbers, enabling computational capabilities beyond classical computers.

In fluid dynamics, complex analysis provides powerful tools for solving problems involving potential flow. The complex potential combines velocity potential and stream function into a single complex-valued function, simplifying the mathematical analysis of fluid flow around objects like airplane wings. Conformal mapping techniques use complex functions to transform difficult flow problems into simpler ones.

These applications demonstrate that imaginary numbers are not just mathematical curiosities but essential tools for understanding and manipulating the physical world. Their “imaginary” nature is purely a historical artifact of their discovery—they are as real and useful as any other mathematical concept that helps us describe and predict natural phenomena.