Pi is more than 3.14; it’s a universal constant that appears everywhere.
What is Pi? Defining the Iconic Ratio of a Circle’s Circumference to Its Diameter
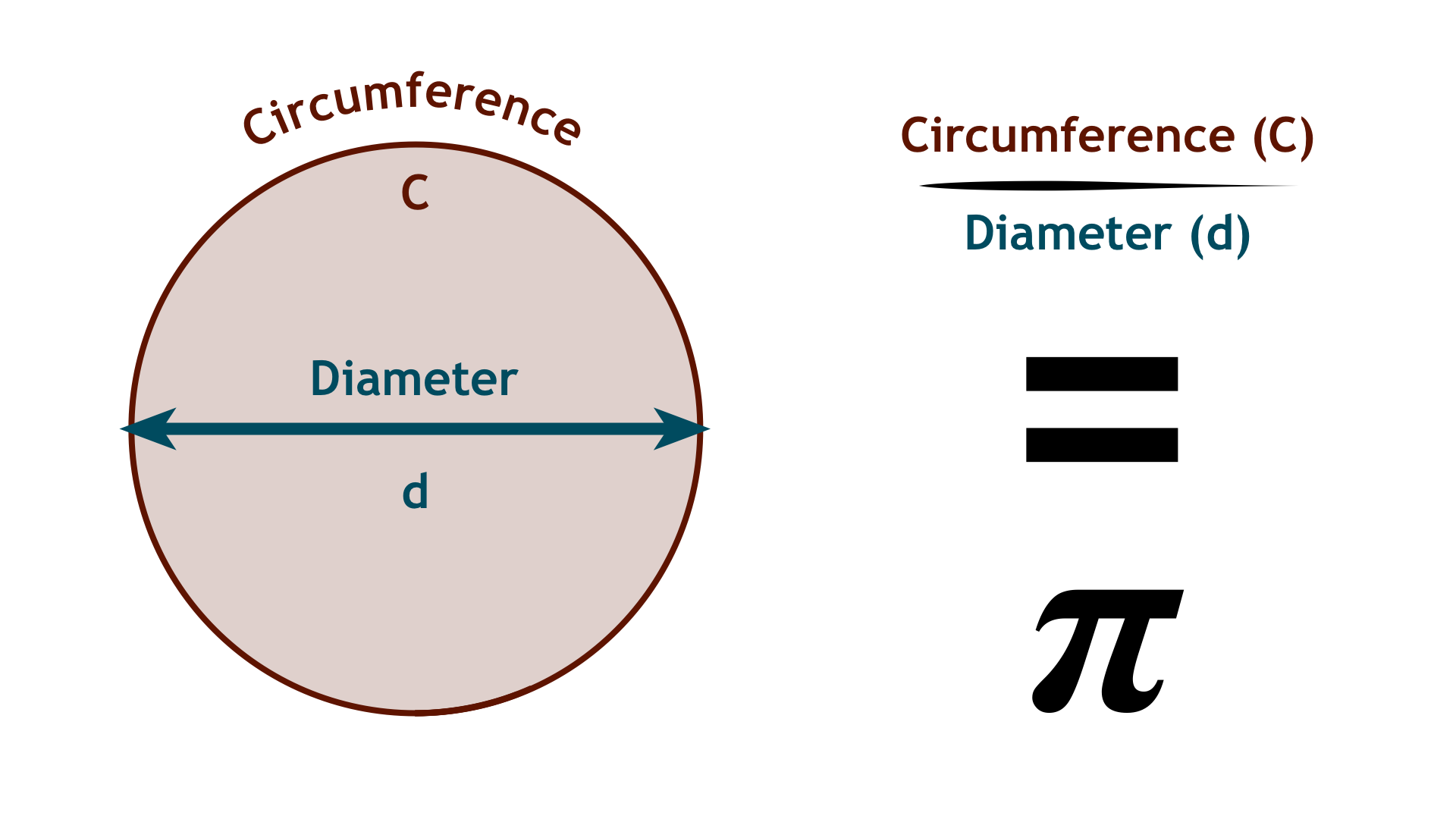
Pi (π) is perhaps the most recognized mathematical constant, known to people worldwide as approximately 3.14159. But what exactly is pi, and why is it so fundamental to mathematics and science? At its core, pi is defined as the ratio of a circle’s circumference to its diameter. This simple geometric relationship reveals a profound mathematical constant that appears throughout nature and human knowledge.
The mathematical definition of pi is elegant in its simplicity: π = C/d, where C is the circumference of a circle and d is its diameter. This ratio remains constant regardless of the circle’s size—a small coin and a giant wheel both have the same pi ratio. This invariance under scaling is a fundamental property that makes pi a universal constant.
The relationship can also be expressed as C = πd or C = 2πr, where r is the radius. These formulas are essential in geometry, engineering, and physics calculations involving circular motion, waves, and periodic phenomena. The constant appearance of 2π in these formulas has led some mathematicians to advocate for tau (τ = 2π) as a more natural constant, representing the ratio of circumference to radius.
Pi also appears in the formula for a circle’s area: A = πr². This relationship can be derived by dividing a circle into infinitesimally thin sectors and rearranging them into a shape that approximates a rectangle with width πr and height r. The mathematical limit of this process as the sectors become infinitely thin gives the exact area formula.
Historically, civilizations recognized pi’s importance long before rigorous mathematical proofs were developed. Ancient Egyptians used an approximation of 22/7 (approximately 3.142857) in the construction of the pyramids. Babylonian mathematicians used 25/8 (3.125), while ancient Chinese mathematicians developed increasingly accurate approximations, including 355/113, which is accurate to six decimal places.
The mathematical quest to calculate pi more precisely has driven mathematical innovation for millennia. Archimedes used the method of exhaustion, inscribing and circumscribing polygons around circles to establish bounds for pi. By using 96-sided polygons, he proved that 223/71 < π < 22/7, giving the approximation 3.14185 with remarkable accuracy for the 3rd century BCE.
In modern mathematics, pi is defined analytically rather than geometrically. Infinite series representations, such as the Leibniz formula π/4 = 1 – 1/3 + 1/4 – 1/5 + 1/7 – …, provide methods for calculating pi to arbitrary precision. However, this series converges slowly, requiring many terms for high accuracy. More efficient formulas, like Ramanujan’s series, converge much more rapidly.
The mathematical constant e (approximately 2.71828) and pi are connected through Euler’s identity: e^(iπ) + 1 = 0, where i is the imaginary unit. This equation, often called the most beautiful in mathematics, connects five fundamental constants (0, 1, e, π, i) through three basic operations (addition, multiplication, exponentiation).
Pi’s geometric definition extends to higher dimensions. In three dimensions, the ratio of a sphere’s surface area to the area of its greatest circle is 4, leading to the formula A = 4πr² for a sphere’s surface area. The volume of a sphere is V = (4/3)πr³, showing how pi appears in three-dimensional geometry.
In non-Euclidean geometries, the ratio of circumference to diameter is not constant and depends on the size of the circle relative to the space’s curvature. However, in the limit of infinitesimally small circles, this ratio approaches π, demonstrating that pi is a local geometric property that transcends specific geometric systems.
The mathematical definition of pi also appears in trigonometry, where 180 degrees equals π radians. This relationship makes π fundamental to angular measurement and periodic functions. The sine and cosine functions have periods of 2π, directly connecting pi to wave phenomena and oscillatory motion.
In calculus, pi emerges from integration formulas. The integral of 1/(1+x²) from -∞ to ∞ equals π, and the Gaussian integral ∫e^(-x²)dx from -∞ to ∞ equals √π. These connections show how pi arises naturally from mathematical analysis, not just geometry.
Understanding pi’s definition as a geometric ratio reveals why it appears so ubiquitously in mathematics and science. Any phenomenon involving circular motion, spherical symmetry, or periodic behavior will naturally involve pi. This geometric foundation makes pi one of the most fundamental constants in mathematics and physics.
An Irrational Number: What It Means for Its Digits to Go On Forever Without Repeating
One of pi’s most fascinating properties is that it’s an irrational number, meaning its decimal representation goes on forever without repeating. This mathematical characteristic distinguishes pi from rational numbers like 1/3 (0.333…) or 22/7 (3.142857142857…), whose decimal expansions eventually repeat. The proof that pi is irrational is a beautiful example of mathematical reasoning that reveals deep truths about numbers.
An irrational number cannot be expressed as a ratio of two integers (a fraction). While rational numbers can always be written as p/q where p and q are integers and q ≠ 0, irrational numbers cannot. This mathematical distinction has profound implications for the structure of the real number system and the nature of mathematical measurement.
The proof that pi is irrational was first accomplished by Johann Lambert in 1768, nearly 2,000 years after pi’s discovery. Lambert showed that if x is a non-zero rational number, then tan(x) must be irrational. Since tan(π/4) = 1 (a rational number), π/4 must be irrational, which means π is irrational. This indirect proof demonstrates the sophisticated mathematical techniques required to establish fundamental properties of constants.
Irrational numbers have decimal expansions that neither terminate nor eventually repeat. This mathematical property means that no matter how far you calculate the digits of pi, you’ll never find a pattern that repeats indefinitely. The digits 3.14159265358979323846… continue infinitely without any repeating cycle.
The mathematical concept of normality relates to the distribution of digits in irrational numbers. A normal number has digits that are uniformly distributed—each digit from 0 to 9 appears with equal frequency (10%), each pair of digits appears with frequency 1%, and so on. While pi hasn’t been proven to be normal, statistical analysis of its computed digits suggests it behaves like a normal number.
Pi’s irrationality has practical implications for measurement and calculation. Since we can only work with finite approximations of pi, all calculations involving pi are approximations. This mathematical reality affects engineering, physics, and computer science, where the precision of pi-based calculations is limited by computational resources.
The mathematical set of irrational numbers is uncountably infinite, meaning there are “more” irrational numbers than rational numbers. This counterintuitive result, proven by Georg Cantor, shows that while we can list all rational numbers in a sequence, we cannot do the same for irrational numbers. Pi is just one of the uncountably many irrational numbers.
Algebraic numbers are solutions to polynomial equations with integer coefficients. For example, √2 is algebraic because it solves x² – 2 = 0. Pi, however, is not just irrational but transcendental, meaning it’s not the solution to any polynomial equation with integer coefficients. This mathematical property makes pi even more special among irrational numbers.
The mathematical proof that pi is transcendental was accomplished by Ferdinand von Lindemann in 1882. This result proved that the ancient problem of “squaring the circle” (constructing a square with the same area as a given circle using only compass and straightedge) is impossible. The transcendental nature of pi means it cannot be constructed with these classical tools.
Irrational numbers like pi fill in the gaps between rational numbers on the real number line. Between any two rational numbers, there are infinitely many irrational numbers, and between any two irrational numbers, there are infinitely many rational numbers. This mathematical property creates the continuous real number line that underlies calculus and analysis.
The infinite, non-repeating nature of pi’s digits has fascinated mathematicians and the public alike. Mathematicians have calculated pi to over 62 trillion digits as of 2021, yet no pattern emerges. This mathematical reality demonstrates that complexity and randomness can arise from simple definitions.
In computer science, the apparent randomness of pi’s digits has been used for pseudo-random number generation and cryptographic applications. While not truly random, the mathematical properties of pi’s expansion make it useful for algorithms that require unpredictable sequences.
The mathematical study of irrational numbers like pi has led to deep insights about the nature of infinity, continuity, and the structure of mathematical systems. These abstract concepts have practical applications in fields from signal processing to quantum mechanics, showing how pure mathematical investigation can lead to technological advances.
Understanding that pi is irrational emphasizes the limitations and approximations inherent in mathematical modeling of the physical world. While we can describe circles and periodic phenomena with great precision using pi, perfect mathematical circles exist only in abstraction, not in physical reality.
Where Pi Shows Up: From Waves and Cycles to Probability
Pi’s appearance extends far beyond circles and geometry, showing up in unexpected places throughout mathematics, physics, and nature. This ubiquitous presence reveals fundamental connections between seemingly unrelated phenomena and demonstrates why pi is considered one of the most important mathematical constants. The appearance of pi in diverse contexts is not coincidence but reflects deep mathematical relationships.
Trigonometric functions are fundamentally connected to pi through their periodic nature. The sine and cosine functions have periods of 2π, meaning sin(x + 2π) = sin(x) for any value of x. This mathematical relationship connects pi to wave phenomena, oscillations, and anything that exhibits periodic behavior. Sound waves, light waves, and alternating current all involve pi in their mathematical descriptions.
Euler’s formula, e^(ix) = cos(x) + i·sin(x), beautifully connects pi with exponential functions and complex numbers. When x = π, this becomes Euler’s identity: e^(iπ) + 1 = 0, relating five fundamental mathematical constants in a single equation. This mathematical relationship underlies much of electrical engineering, signal processing, and quantum mechanics.
In probability and statistics, pi appears in the normal distribution (bell curve), one of the most important probability distributions. The probability density function for a standard normal distribution is f(x) = (1/√(2π)) · e^(-x²/2). The √(2π) normalization factor ensures that the total probability integrates to 1, connecting pi to the mathematical foundations of statistics.
Buffon’s needle problem is a classic probability experiment that directly estimates pi. If you drop a needle of length L onto a floor with parallel lines spaced distance D apart, the probability that the needle crosses a line is 2L/(πD). By conducting many trials, you can estimate pi statistically. This mathematical connection between geometry and probability is surprising and elegant.
In physics, pi appears in formulas describing wave phenomena, including the wave equation that governs sound, light, and water waves. The mathematical solutions to these equations involve sinusoidal functions with arguments that include pi, reflecting the periodic nature of wave motion.
Quantum mechanics, the mathematical framework describing atomic and subatomic phenomena, is filled with pi. The Heisenberg uncertainty principle, Schrödinger equation, and wave functions all involve pi in their mathematical formulations. The spherical harmonics that describe electron orbitals in atoms contain pi in their normalization factors.
In Fourier analysis, which decomposes complex waveforms into simpler sinusoidal components, pi appears naturally in the mathematical transforms. The Fourier transform of a Gaussian function involves pi, and the mathematical theory of signal processing relies heavily on pi’s properties.
General relativity, Einstein’s theory of gravitation, includes pi in the Einstein field equations that relate the curvature of spacetime to matter and energy. The mathematical constant 8πG/c⁴ appears in these equations, where G is the gravitational constant and c is the speed of light.
In number theory, pi appears in Euler’s solution to the Basel problem: the sum of the reciprocals of the squares of positive integers equals π²/6. This mathematical result connects the discrete world of integers with the continuous constant pi in an unexpected way.
Pi also appears in the mathematical formulas for the volumes and surface areas of higher-dimensional spheres. In n-dimensional space, the volume of a unit sphere involves π^(n/2) divided by the gamma function. For example, the volume of a 4-dimensional sphere is π²/2, showing how pi generalizes beyond three-dimensional geometry.
In complex analysis, the mathematical study of functions of complex variables, pi appears in Cauchy’s integral formula and the residue theorem. These fundamental results in mathematical analysis connect the behavior of complex functions to integrals involving pi.
The mathematical constant pi even appears in the formulas for the period of a simple pendulum and the motion of harmonic oscillators. For small oscillations, the period T = 2π√(L/g), where L is the pendulum length and g is gravitational acceleration. This mathematical relationship connects pi to the fundamental physics of oscillatory motion.
In engineering applications, pi appears in formulas for calculating stress and strain in circular structures, fluid dynamics in pipes, and electromagnetic field calculations. The mathematical constant is essential for designing everything from bridges to electronic circuits.
The appearance of pi in so many diverse contexts illustrates a fundamental principle in mathematics and science: seemingly different phenomena often share deep mathematical structures. Pi’s ubiquity reflects the underlying unity of mathematical laws that govern everything from the smallest quantum effects to the largest cosmic structures.
Conclusion: Pi’s Mysterious and Essential Role in Describing Our Universe
Pi transcends its simple geometric definition as the ratio of a circle’s circumference to its diameter to become a fundamental constant that appears throughout mathematics and science. Its irrational and transcendental nature reveals deep mathematical truths about the structure of numbers and the limits of geometric construction. The unexpected appearance of pi in probability, quantum mechanics, and number theory demonstrates mysterious connections between seemingly unrelated areas of knowledge.
The mathematical properties of pi continue to fascinate and challenge mathematicians. Its normality (whether all digits appear with equal frequency) remains unproven, and its computational complexity continues to drive algorithmic development. The quest to calculate more digits of pi has pushed the boundaries of computational mathematics and revealed properties of algorithms and computer systems.
Pi’s role in describing our universe extends from the most fundamental physical laws to practical engineering applications. Its presence in wave equations connects it to all oscillatory phenomena, from the vibrations of guitar strings to the propagation of radio waves. In quantum mechanics, pi connects the mathematical formalism to observable reality, making it essential for understanding atomic and subatomic behavior.
The cultural significance of pi extends beyond mathematics to become a symbol of human curiosity and the quest for knowledge. Pi Day (March 14th, 3/14) celebrates mathematics education and shows how abstract mathematical concepts can capture public imagination. The mathematical constant represents the beauty and elegance that emerge from rigorous logical reasoning.
Most importantly, pi exemplifies how mathematics reveals hidden patterns and connections in nature. Its ubiquitous presence suggests that mathematical relationships are not human inventions but discoveries of underlying principles that govern reality. Pi’s journey from ancient geometry to modern physics demonstrates the power of mathematical thinking to uncover universal truths and provides a glimpse into the deep mathematical structure of our universe.