The Birthday Paradox: The Odds Are Not What You Think

The birthday paradox is one of the most counterintuitive results in probability theory, illustrating how our brains struggle with combinatorial reasoning and the difference between specific and general probabilities. When told that in a group of just 23 people there’s a better than 50% chance that two people share the same birthday, most people find this result shocking. Our intuition tells us that with 365 possible birthdays, we’d need many more people to have a reasonable chance of a match. But our intuition is wrong, and understanding why reveals important insights about probability and human cognition.

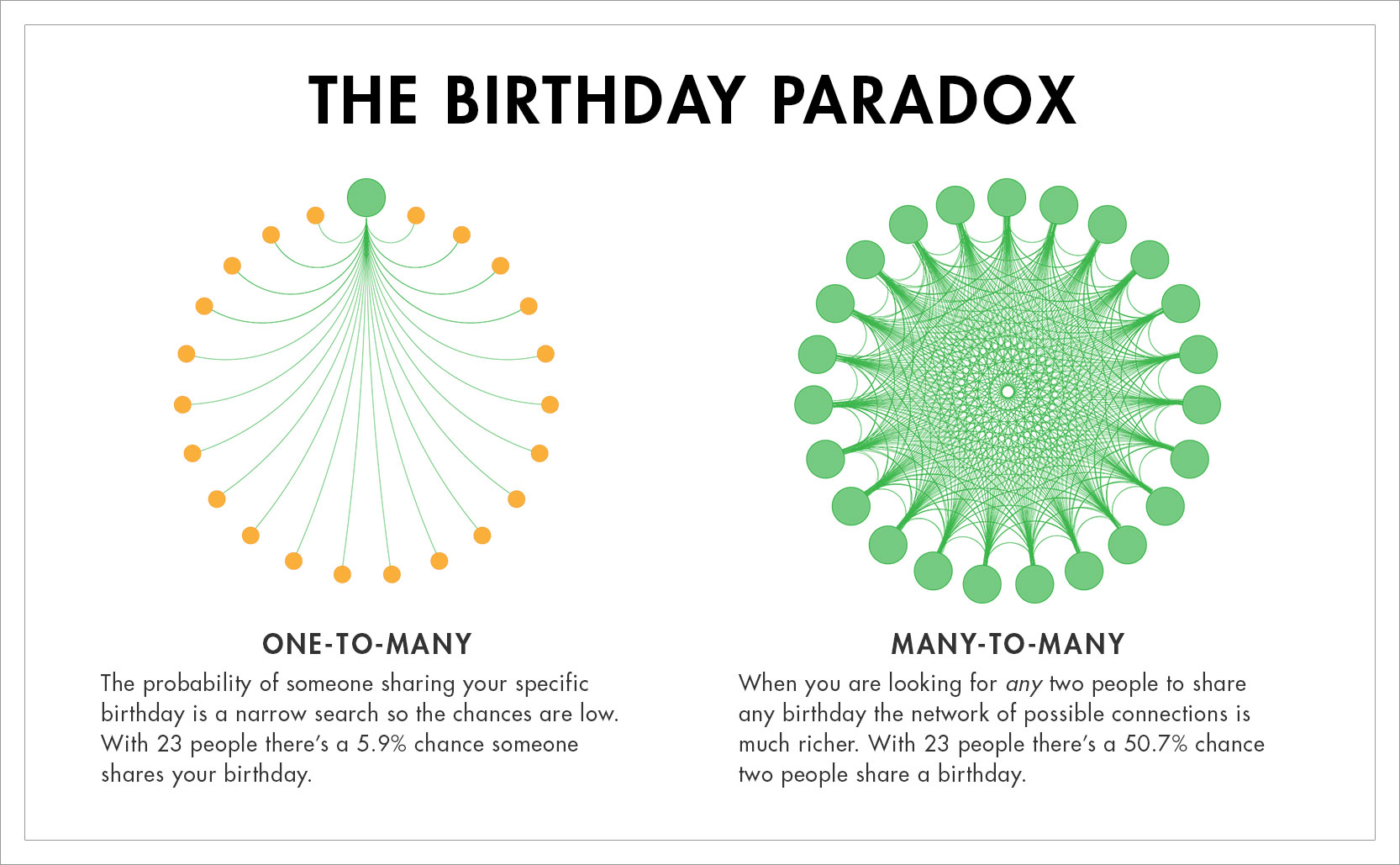
The key to understanding the birthday paradox lies in recognizing the difference between two distinct probability questions. The first question, which our intuition tends to focus on, is: “What is the probability that someone in this group shares a specific birthday with me (e.g., January 1st)?” This probability increases linearly with the number of people in the group. With 23 people, the probability that at least one shares your specific birthday is only about 6%.

The second question, which leads to the paradoxical result, is: “What is the probability that any two people in this group share the same birthday (regardless of which day it is)?” This is a fundamentally different question that involves comparing all possible pairs of people in the group. With 23 people, there are 23×22/2 = 253 different pairs, which dramatically increases the chances of finding a match.

Our cognitive bias toward the first interpretation stems from how we naturally think about coincidences. When we meet someone who shares our birthday, it feels remarkably unlikely and special. We focus on this specific match rather than considering all the other possible matches that could occur. This egocentric bias leads us to underestimate the probability of any match occurring in a group.

The mathematical concept of combinatorial explosion also contributes to our misunderstanding. As the number of people in a group increases, the number of possible pairs grows quadratically rather than linearly. With n people, there are n(n-1)/2 possible pairs. This rapid growth means that even with a relatively small group, the number of comparisons becomes substantial.

Another factor that confounds our intuition is the availability heuristic—we judge the probability of events based on how easily we can recall examples. Since we rarely hear about birthday matches in small groups, we assume they’re rare. However, this lack of memorable examples doesn’t reflect the actual mathematical probability; it reflects our limited exposure to all the groups where matches do occur.

The representativeness heuristic also plays a role. We tend to think that a “random” distribution of birthdays should look evenly spread throughout the year. When we learn that 23 people have a 50% chance of sharing a birthday, it seems to violate our mental model of randomness. In reality, true randomness often produces seemingly non-random clustering.

Our experience with small numbers also misleads us. In our daily lives, we rarely encounter groups where we can observe the birthday paradox in action. Most social groups we’re part of are much smaller than 23 people, so we don’t have intuitive experience with the phenomenon. This lack of direct experience makes the mathematical result seem implausible.

The birthday paradox also illustrates the difference between mathematical probability and subjective belief. Mathematically, the probabilities can be calculated precisely, but our subjective assessment of the situation may differ significantly. This disconnect between objective mathematical truth and subjective perception is at the heart of many probability paradoxes.

Cultural factors may influence our understanding as well. In many societies, sharing a birthday is considered special or fated, which may make us think of birthday matches as rarer than they actually are. This cultural significance can bias our probabilistic reasoning.

Understanding why our brains get the birthday paradox wrong is valuable for developing better decision-making skills. It teaches us to question our assumptions, consider all possible outcomes, and recognize when our cognitive biases might be leading us astray. These skills extend far beyond birthday parties to important real-world decisions involving risk assessment and probability judgment.

The mathematical lesson is that intuition, while often helpful, can be misleading in probability problems involving combinations and large numbers of possibilities. Developing facility with formal probability methods—like complementary probability and combinatorial analysis—provides more reliable tools for analyzing uncertain situations. The birthday paradox serves as a memorable example of why these mathematical tools are necessary.

To understand why 23 people give us a 50% chance of a shared birthday, we need to work through the mathematical calculation step by step. The key insight is to calculate the probability of NO shared birthdays and then subtract from 1 to get the probability of at least one shared birthday. This complementary probability approach is often easier than calculating the probability of shared birthdays directly.

Let’s start with a simple case: two people. We want to find the probability that they have different birthdays. Assuming a non-leap year with 365 days, the first person can have any birthday (probability 365/365 = 1). The second person must have a different birthday, so they have 364 choices out of 365 possible days. The probability of different birthdays is:

Therefore, the probability of a shared birthday is 1 – 0.9973 = 0.0027 or about 0.27%.

With three people, we continue the pattern. The first person can have any birthday (365/365). The second person must have a different birthday (364/365). The third person must have a birthday different from both previous people (363/365). The probability of all different birthdays is:

So the probability of at least one shared birthday is 1 – 0.9918 = 0.0082 or about 0.82%.

We can generalize this pattern for n people. The probability that all n people have different birthdays is:

This can be written more compactly using factorial notation:

However, calculating factorials of large numbers like 365! is computationally challenging. A more practical approach is to calculate the product directly:

Let’s compute this for several values of n to see the pattern:

For n = 10 people:

Probability of shared birthday = 1 – 0.8831 = 0.1169 or about 11.7%

For n = 20 people:

Probability of shared birthday = 1 – 0.5886 = 0.4114 or about 41.1%

For n = 23 people:

Probability of shared birthday = 1 – 0.4927 = 0.5073 or about 50.7%

This confirms the surprising result: with just 23 people, there’s slightly better than a 50% chance of a shared birthday.

For n = 30 people:

Probability of shared birthday = 1 – 0.2937 = 0.7063 or about 70.6%

For n = 50 people:

Probability of shared birthday = 1 – 0.0296 = 0.9704 or about 97.0%

The mathematical calculation also reveals the rapid increase in probability as group size grows. The transition from low probability to high probability happens quickly around the 20-25 person range, which is why 23 is the critical number for the 50% threshold.

We can also derive an approximation formula for large groups. Using the approximation that for small x, ln(1-x) ≈ -x, we can approximate:

Therefore:

Setting this equal to 0.5 and solving for n gives n ≈ √(2×365×ln(2)) ≈ 22.5, which confirms our exact calculation.

The mathematical analysis also extends to variations of the problem. If we want to know the probability that someone shares a specific birthday (like yours), the calculation is different. With n people, the probability that none of them share your specific birthday is (364/365)^n. To have a 50% chance that someone shares your birthday, we need (364/365)^n = 0.5, which gives n ≈ 253 people—much larger than 23!

This mathematical framework can be applied to other “coincidence” problems. For example, in a group of people, what’s the probability that two have phone numbers ending in the same digit? With 10 possible endings, the calculation is similar but with 10 instead of 365, so you only need about √(2×10×ln(2)) ≈ 3.7 people for a 50% chance.

Understanding these mathematical calculations provides insight into probability theory, combinatorics, and the behavior of random processes. These concepts are fundamental to statistics, computer science, cryptography, and many other fields. The birthday paradox serves as an accessible introduction to these important mathematical ideas.

The birthday paradox is far more than a mathematical curiosity—it has profound and practical applications in computer science, cryptography, and information security. The underlying principle that the probability of a collision (two items having the same value) increases much faster than intuition suggests is fundamental to many modern technologies and security protocols.

In computer science, the birthday paradox is essential for understanding hash functions, which map data of arbitrary size to fixed-size values. Hash functions are used extensively in data structures like hash tables for efficient data retrieval. The birthday paradox tells us that even with a large hash space, collisions are more likely than we might expect. For example, with a 32-bit hash function (4 billion possible values), we only need about √(2×4×10⁹×ln(2)) ≈ 77,000 items before there’s a 50% chance of a collision.

This understanding is crucial for designing hash tables and choosing appropriate hash functions. Computer scientists use the birthday paradox to determine the expected number of collisions and to size hash tables appropriately. When the number of items approaches the square root of the hash space size, the collision rate increases dramatically, degrading performance.

In cryptography, the birthday paradox leads to the concept of birthday attacks on hash functions. A cryptographic hash function should be collision-resistant, meaning it should be computationally infeasible to find two different inputs that produce the same output. However, the birthday paradox shows that finding any collision requires only about √(π×N/2) attempts, where N is the size of the hash space, rather than N attempts to find a specific collision.

For example, a 128-bit hash function has 2¹²⁸ possible outputs, which seems enormous. However, a birthday attack can find a collision in about √(2¹²⁸) = 2⁶⁴ attempts, which is significantly smaller. This is why cryptographic hash functions often have larger output sizes than might seem necessary—256-bit or 512-bit hashes—to ensure security against birthday attacks.

Digital signature schemes are particularly vulnerable to birthday attacks. An attacker could prepare two documents, one legitimate and one fraudulent, that hash to the same value. If they can get someone to sign the legitimate document, that signature would also be valid for the fraudulent document. The birthday paradox makes this attack feasible with much less computational effort than finding a specific collision.

Random number generators are also analyzed using birthday paradox principles. Cryptographically secure random number generators should produce outputs that are indistinguishable from truly random sequences. Statistical tests based on the birthday paradox can detect non-randomness in pseudorandom number generators by looking for unexpected collision rates.

In network security, the birthday paradox affects the design of protocols that use random identifiers. For example, in distributed systems, nodes often generate random IDs to avoid conflicts. The birthday paradox helps system designers understand how large the ID space needs to be to keep collision probabilities acceptably low.

Blockchain technology relies on cryptographic hash functions, making birthday attacks a significant concern. The security of blockchain systems depends on the computational difficulty of finding hash collisions. Understanding the birthday paradox is crucial for assessing the security of different blockchain implementations and choosing appropriate hash functions.

Database systems use the birthday paradox to optimize query performance and index design. When multiple records might hash to the same index location, understanding collision probabilities helps database designers choose appropriate hash functions and table sizes to maintain performance.

In machine learning, hash functions are used for dimensionality reduction and approximate algorithms. The birthday paradox helps researchers understand the trade-offs between hash space size, collision probability, and computational efficiency in algorithms like locality-sensitive hashing.

Password security also involves birthday paradox considerations. When storing password hashes, systems need to consider the probability of hash collisions, especially when using older or smaller hash functions. Modern password hashing uses techniques like salting to prevent birthday attacks.

The birthday paradox even appears in quantum computing research. Quantum algorithms for finding collisions can achieve a quadratic speedup over classical algorithms, directly related to the square root relationship in the birthday paradox. This has implications for the security of cryptographic systems against quantum attacks.

Understanding the birthday paradox has led to the development of more secure cryptographic protocols and better system designs. It’s a prime example of how abstract mathematical concepts can have concrete, practical implications for technology and security. The paradox reminds us that our intuitions about probability can be misleading, especially in systems with large state spaces, and that rigorous mathematical analysis is essential for secure system design.