The Seven Bridges of Königsberg: The Puzzle That Created a New Math

The Seven Bridges of Königsberg problem is one of the most famous puzzles in the history of mathematics, not because of its complexity, but because of its profound impact on the development of mathematical thinking. This seemingly simple recreational problem, posed in the 18th century Prussian city of Königsberg (now Kaliningrad, Russia), led to the creation of an entirely new branch of mathematics: graph theory. The problem demonstrates how a practical, everyday question can give birth to abstract mathematical concepts with far-reaching applications.

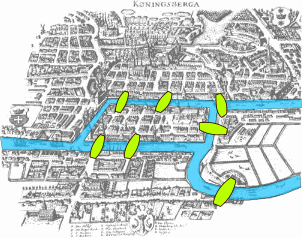
Königsberg was built on both sides of the Pregel River, including two large islands, Kneiphof and Lomse, connected to each other and to the mainland by seven bridges. The citizens of Königsberg reportedly spent their Sunday afternoons trying to solve a recreational puzzle: Was it possible to take a walk through the city that would cross each bridge exactly once and return to the starting point? This challenge became a popular local pastime, with many residents attempting to find such a path through trial and error.

The geographical layout of Königsberg was crucial to the problem. The city consisted of four distinct landmasses: the north bank, the south bank, the Kneiphof island, and the Lomse island. These landmasses were connected by seven bridges: the Blacksmith’s Bridge, the Connecting Bridge, the Green Bridge, the Merchant’s Bridge, the Wooden Bridge, the High Bridge, and the Honey Bridge. Each bridge connected exactly two landmasses, and the challenge was to find a continuous path that crossed each bridge exactly once.

The mathematical nature of the problem wasn’t immediately apparent to the citizens of Königsberg. They approached it as a practical challenge, attempting to trace routes on maps or actually walking through the city trying different sequences. Many claimed to have found solutions, but upon careful examination, these supposed solutions always involved crossing some bridges multiple times or missing others entirely. The problem proved remarkably resistant to solution by trial and error.

The problem attracted the attention of Leonhard Euler, one of the most prolific mathematicians in history, when he was working at the St. Petersburg Academy of Sciences. Euler was known for his ability to find mathematical structure in seemingly unrelated problems, and the Königsberg bridge problem was no exception. Rather than attempting to solve the problem through exhaustive search, Euler sought to understand its underlying mathematical principles.

Euler’s insight was to abstract the problem by focusing on the essential elements: the landmasses and the bridges connecting them. He realized that the exact shape of the landmasses, the length of the bridges, and the distances between them were irrelevant to the problem. What mattered was only which landmasses were connected to which others, and by how many bridges. This abstraction was revolutionary in mathematical thinking.

In modern terms, Euler represented the problem as a graph, with vertices (nodes) representing the landmasses and edges (lines) representing the bridges. This representation stripped away all unnecessary geographical details, reducing the problem to its mathematical essence. The Kneiphof island, Lomse island, north bank, and south bank became four vertices, and the seven bridges became seven edges connecting these vertices in specific patterns.

The problem then became: Is there a path through this graph that traverses each edge exactly once and returns to the starting vertex? Such a path is now called an Eulerian circuit, in Euler’s honor. If the path doesn’t need to return to the starting point, it’s called an Eulerian path. Euler’s analysis of when such paths exist laid the foundation for graph theory.

The specific arrangement of bridges in Königsberg created a graph with four vertices, with the following degrees (number of edges connected to each vertex): Kneiphof had degree 5 (connected to 5 bridges), Lomse had degree 3, the north bank had degree 3, and the south bank had degree 3. Euler’s solution would reveal that this particular arrangement made the desired path impossible.

The problem’s resistance to solution by trial and error illustrates an important principle in mathematics: when a problem seems intractable through brute force methods, it often requires a new perspective or abstraction. Euler’s approach of transforming a geographical problem into a combinatorial one was a paradigm shift that opened up new avenues of mathematical investigation.

The Seven Bridges problem also demonstrates how recreational mathematics can lead to serious mathematical developments. Euler wasn’t motivated by practical concerns about bridge maintenance or city planning; he was intrigued by the logical structure of the problem itself. This curiosity-driven approach to mathematics has led to many of the field’s most important discoveries.

Understanding the historical context of the problem also reveals how mathematical thinking has evolved. In Euler’s time, the connection between geometry and combinatorics was not as well understood as it is today. The idea that a geographical problem could be reduced to a study of connections and relationships was innovative and would prove to be extremely fruitful.

The Königsberg bridge problem serves as a perfect example of how mathematics often begins with concrete, real-world problems but develops into abstract theories with applications far beyond their original context. The graph theory born from this puzzle would later become essential for understanding computer networks, social connections, transportation systems, and countless other phenomena.

Leonhard Euler’s solution to the Königsberg bridge problem was a masterclass in mathematical abstraction and problem-solving. Rather than attempting to find a path through the physical city, Euler transformed the problem into a purely mathematical question about connections and relationships. His approach was so innovative that it created an entirely new branch of mathematics: graph theory, which has since become fundamental to computer science, network analysis, and many other fields.

Euler’s key insight was that the exact geographical layout of Königsberg was irrelevant to the problem. The distances between landmasses, the lengths of bridges, and the winding paths through the city were all distractions from the essential mathematical structure. What mattered was only the pattern of connections: which landmasses were connected to which others, and by how many bridges. This realization allowed Euler to strip away all unnecessary details and focus on the core mathematical relationships.

In his 1736 paper “Solutio problematis ad geometriam situs pertinentis” (The solution of a problem relating to the geometry of position), Euler introduced a revolutionary way of representing the problem. He replaced each landmass with a point (now called a vertex or node) and each bridge with a line (now called an edge) connecting two points. This abstract representation, which we now call a graph, captured all the relevant information while eliminating all irrelevant geographical details.

Euler’s graph representation consisted of four vertices representing the four landmasses of Königsberg: the Kneiphof island, the Lomse island, the north bank, and the south bank. The seven edges represented the seven bridges connecting these landmasses. The Kneiphof island was connected to the north bank by two bridges, to the south bank by two bridges, and to the Lomse island by one bridge. The Lomse island was connected to the north bank by one bridge and to the south bank by one bridge.

With this abstraction, Euler reformulated the problem: Is it possible to draw a path through the graph that traverses each edge exactly once? This is now known as finding an Eulerian path. If the path must start and end at the same vertex, it’s called an Eulerian circuit. Euler’s genius lay in recognizing that this reformulation made the problem tractable through logical analysis rather than trial and error.

Euler then developed a systematic approach to determine when such paths exist. He focused on what happens at each vertex during a traversal of the graph. Except for the starting and ending vertices of an Eulerian path, every time you enter a vertex, you must also leave it. This means that for any intermediate vertex, the number of edges entering it must equal the number of edges leaving it, so the total degree (number of edges connected to the vertex) must be even.

For an Eulerian circuit, where the path starts and ends at the same vertex, this argument applies to all vertices. Every time you enter a vertex, you must leave it, so all vertices must have even degree. For an Eulerian path that doesn’t return to its starting point, exactly two vertices can have odd degree: the starting vertex (where you leave one more time than you enter) and the ending vertex (where you enter one more time than you leave).

Euler’s theorem states that a connected graph has an Eulerian circuit if and only if every vertex has even degree, and it has an Eulerian path if and only if exactly zero or two vertices have odd degree. This elegant characterization provides a simple algorithm for determining the existence of Eulerian paths without having to search through all possible paths.

Applying this theorem to the Königsberg graph, Euler counted the degrees of each vertex: Kneiphof had degree 5, Lomse had degree 3, the north bank had degree 3, and the south bank had degree 3. Since all four vertices had odd degree, Euler’s theorem showed that neither an Eulerian circuit nor an Eulerian path was possible. The popular recreational puzzle had no solution.

Euler’s solution was remarkable not just for its answer but for its method. He had transformed a geographical problem into a problem in what he called the “geometry of position” (geometria situs), now known as topology and graph theory. This approach of studying properties that remain unchanged under continuous deformation (like stretching or bending, but not cutting or gluing) was revolutionary and would prove to be extremely fruitful.

The mathematical elegance of Euler’s solution lies in its generality. Rather than solving just the Königsberg problem, Euler had developed a method that could be applied to any similar problem. Given any arrangement of landmasses and bridges, one could construct the corresponding graph, count vertex degrees, and immediately determine whether an Eulerian path exists.

Euler also considered the broader implications of his approach. He noted that the same method could be applied to problems involving the traversal of any network of connections, whether representing bridges, roads, or abstract relationships. This insight would prove prophetic, as graph theory has become essential for understanding everything from computer networks to social media connections.

The solution also demonstrated the power of mathematical abstraction. By removing all non-essential details and focusing on the core relationships, Euler had made a seemingly intractable problem completely transparent. This approach of finding the essential mathematical structure in real-world problems has become a fundamental technique in applied mathematics.

Euler’s work on the Königsberg bridges problem is considered the first theorem in graph theory and the first true theorem in topology. It established the foundation for these fields and demonstrated how abstract mathematical thinking could solve concrete problems. The paper is still studied today as a masterpiece of mathematical reasoning and abstraction.

Euler’s solution to the Königsberg bridge problem wasn’t just an answer to a recreational puzzle—it was the birth of graph theory, a mathematical discipline that has become fundamental to computer science, network analysis, operations research, and countless other fields. The simple rule Euler discovered provides a complete characterization of when it’s possible to traverse every edge of a graph exactly once, solving not just the Königsberg problem but any similar problem involving networks of connections.

Euler’s fundamental theorem states that a connected graph has an Eulerian circuit (a closed path that traverses each edge exactly once) if and only if every vertex has even degree. A graph has an Eulerian path (a path that traverses each edge exactly once but doesn’t need to return to the starting point) if and only if exactly zero or two vertices have odd degree. This elegant characterization completely solves the problem and provides a simple algorithm for determining the existence of such paths.

To understand why this rule works, consider what happens during a traversal of a graph. At any intermediate vertex (not the start or end), every time you enter the vertex, you must also leave it. This means that the edges at that vertex must come in pairs: one for entering and one for leaving. Therefore, the total number of edges connected to any intermediate vertex must be even, which means the vertex has even degree.

For an Eulerian circuit, the path starts and ends at the same vertex, so that vertex is also intermediate in the sense that it’s entered and left the same number of times. Therefore, all vertices in an Eulerian circuit must have even degree. Conversely, if all vertices have even degree, it’s possible to construct an Eulerian circuit by systematically traversing edges while ensuring that no edge is used twice.

For an Eulerian path that doesn’t return to its starting point, exactly two vertices can have odd degree: the starting vertex (where you leave one more time than you enter) and the ending vertex (where you enter one more time than you leave). All other vertices must have even degree for the same reason as in the circuit case.

Euler’s rule provides a simple algorithm for any bridge-traversal problem:

1. Represent the problem as a graph with vertices for landmasses and edges for bridges
2. Count the degree (number of edges) of each vertex
3. If all vertices have even degree, an Eulerian circuit exists
4. If exactly two vertices have odd degree, an Eulerian path exists
5. If more than two vertices have odd degree, no such path exists

Applying this algorithm to the Königsberg problem, we find that all four vertices have odd degree (5, 3, 3, and 3), so neither an Eulerian circuit nor an Eulerian path is possible. The popular puzzle has no solution, and Euler’s theorem explains exactly why.

The mathematical beauty of Euler’s theorem lies in its completeness and simplicity. It doesn’t just solve specific problems; it provides a universal method for determining the existence of Eulerian paths in any graph. This generality makes it incredibly powerful and widely applicable.

In computer science, Eulerian paths have applications in designing efficient algorithms for traversing networks. For example, in testing integrated circuits, engineers want to test every connection exactly once, which is essentially finding an Eulerian path in a graph representing the circuit. Euler’s theorem tells them when such a test sequence is possible.

Bioinformatics uses Eulerian paths in DNA sequencing. When sequencing long DNA strands, scientists break them into shorter fragments, sequence the fragments, and then reconstruct the original sequence. This reconstruction problem can be formulated as finding an Eulerian path in a graph where vertices represent DNA fragments and edges represent overlaps between fragments.

Urban planning and transportation engineering apply Eulerian path concepts to design efficient routes for services like garbage collection, street cleaning, and mail delivery. These problems often involve finding ways to traverse every street in a neighborhood exactly once, which is an Eulerian path problem.

In manufacturing, Eulerian paths help optimize the movement of tools in computer-controlled machining operations. When a tool needs to perform operations at various points on a workpiece, finding an Eulerian path through the graph of operations minimizes tool travel time.

Social network analysis uses graph theory concepts derived from Euler’s work to understand connections between people, organizations, and information flows. While Eulerian paths aren’t the primary focus, the foundational concepts of vertices, edges, and connectivity that Euler introduced are essential to the field.

Modern internet and telecommunications networks are analyzed using graph theory. The robustness, efficiency, and vulnerability of these networks can be studied using concepts that trace back to Euler’s original work on connectivity and traversal.

Eulerian paths also appear in recreational mathematics and puzzle design. Many modern puzzles, from maze traversal to logic games, have underlying graph structures where Eulerian path concepts apply. Understanding Euler’s theorem helps both puzzle designers and solvers.

The mathematical framework that Euler established has been extended in countless ways. While his original theorem addressed the existence of Eulerian paths, mathematicians have since developed algorithms for actually constructing such paths when they exist, studied variations of the problem, and generalized the concepts to more complex structures.

Euler’s work demonstrates how abstract mathematical thinking can solve concrete problems and lead to powerful general theories. The simple rule he discovered for Eulerian paths exemplifies the mathematical principle that deep insights often have simple, elegant expressions. This principle continues to guide mathematical research and has proven to be one of the most valuable lessons of Euler’s solution to the Königsberg bridges problem.