Zeno’s Paradoxes: Can You Ever Actually Reach Your Destination?

Zeno of Elea, a pre-Socratic Greek philosopher who lived in the 5th century BCE, formulated a series of paradoxes that have puzzled thinkers for over two millennia. These paradoxes, which challenge our fundamental understanding of motion, space, and time, were designed to support the philosophical teachings of his mentor Parmenides, who argued that reality is unchanging and that motion is an illusion. While Zeno’s conclusions may seem counterintuitive to our everyday experience, his paradoxes reveal deep insights about the nature of infinity, continuity, and mathematical reasoning.

Zeno’s paradoxes are remarkable not only for their philosophical implications but also for their mathematical sophistication. They forced mathematicians and philosophers to grapple with concepts of infinity and continuity long before the development of calculus and modern mathematical analysis. The paradoxes demonstrate how careful logical reasoning can lead to conclusions that seem to contradict our sensory experience, highlighting the complex relationship between mathematical abstraction and physical reality.

Although Zeno’s original works have not survived, his paradoxes were recorded by later philosophers, particularly Aristotle, who discussed them extensively in his “Physics.” Aristotle identified four of Zeno’s paradoxes of motion, though scholars believe Zeno formulated others. The most famous include the Dichotomy Paradox, Achilles and the Tortoise, the Arrow Paradox, and the Stadium Paradox. Each paradox approaches the problem of motion from a different angle, but all challenge the possibility of motion by revealing apparent logical contradictions.

The enduring significance of Zeno’s paradoxes lies in how they expose the limitations of intuitive reasoning about infinity and continuity. Our everyday experience with motion makes it seem obvious that we can move from one place to another, but Zeno’s arguments suggest that this apparent simplicity conceals profound mathematical complexities. These paradoxes have influenced the development of mathematical thinking, leading to more rigorous foundations for calculus and the theory of infinite series.

In the ancient world, Zeno’s paradoxes were primarily philosophical tools designed to support Parmenidean metaphysics. However, their mathematical content has proven to be of lasting importance. They raised questions about the nature of mathematical infinity, the relationship between discrete and continuous quantities, and the foundations of geometry that would not be fully resolved until the development of modern mathematical analysis in the 17th through 19th centuries.

The paradoxes also illustrate the power of reductio ad absurdum, a form of argument that assumes a proposition and then shows that this assumption leads to a contradiction or absurd conclusion. Zeno’s method was to assume that motion is possible and then demonstrate that this assumption leads to logical impossibilities, thereby “proving” that motion is impossible. While we now know that the paradoxes don’t actually prove motion impossible, they do reveal hidden assumptions in our understanding of space, time, and infinity.

Modern interpretations of Zeno’s paradoxes often focus on the mathematical concepts they embody rather than their metaphysical implications. They serve as early examples of thought experiments that use logical reasoning to explore the implications of mathematical concepts. This approach has become a fundamental tool in both philosophy and theoretical science, from Einstein’s relativity to quantum mechanics.

The resolution of Zeno’s paradoxes required the development of new mathematical concepts, particularly the theory of infinite series and the rigorous definition of limits. These mathematical tools showed that infinite processes can have finite outcomes, resolving the apparent contradictions in Zeno’s arguments. This resolution demonstrates how mathematical innovation can address philosophical problems that seem intractable through purely logical reasoning.

Zeno’s paradoxes continue to be relevant in modern discussions of physics and philosophy. They raise questions about the nature of spacetime, the relationship between mathematical models and physical reality, and the foundations of calculus that remain active areas of research. The paradoxes remind us that our intuitive understanding of fundamental concepts can be misleading and that rigorous mathematical analysis is often necessary to resolve apparent contradictions.

The study of Zeno’s paradoxes also illustrates the interconnectedness of mathematics, philosophy, and physics. What began as a philosophical argument about the nature of reality has influenced mathematical thinking and continues to inform our understanding of the physical world. This interdisciplinary impact demonstrates the unity of human knowledge and the value of approaching complex problems from multiple perspectives.

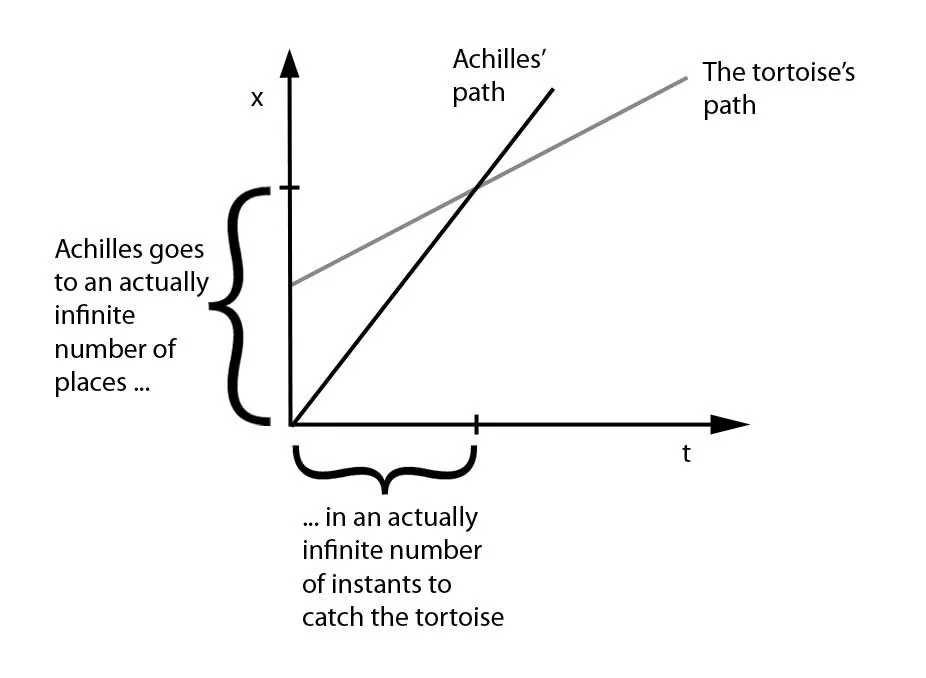
Zeno’s paradox of Achilles and the Tortoise is perhaps the most famous of his paradoxes and one of the most enduring puzzles in the history of mathematics and philosophy. The paradox presents a seemingly simple scenario: Achilles, the legendary Greek hero known for his speed, races against a tortoise, giving the tortoise a head start to make the race fair. Despite being much faster, Achilles can never overtake the tortoise, according to Zeno’s argument. This conclusion contradicts our everyday experience and seems absurd, yet Zeno’s reasoning appears logically sound.

The paradox can be stated as follows: Suppose the tortoise is given a 100-meter head start. Achilles runs at 10 meters per second, while the tortoise moves at 1 meter per second. By the time Achilles reaches the tortoise’s starting point (after 10 seconds), the tortoise has moved 10 meters ahead. When Achilles reaches that point (after 1 more second), the tortoise has moved 1 meter further. This process continues indefinitely, with Achilles always reaching the point where the tortoise was, only to find that the tortoise has moved a bit further. Therefore, Achilles never catches the tortoise.

Zeno’s argument relies on the idea that to reach the tortoise, Achilles must complete an infinite sequence of tasks: reaching the tortoise’s starting point, then where the tortoise was after 10 seconds, then where the tortoise was after 11 seconds, and so on. Since this involves completing an infinite number of tasks, Zeno argued that Achilles could never finish the race. This reasoning seems to prove that motion is impossible, or at least that a faster object can never overtake a slower one.

The mathematical structure of the paradox involves an infinite geometric series. The distances Achilles must cover form the sequence: 100 + 10 + 1 + 1/10 + 1/100 + … This is a geometric series with first term a = 100 and common ratio r = 1/10. The total distance Achilles travels is the sum of this infinite series.

In modern mathematical terms, we know that a geometric series with |r| < 1 converges to a finite sum. The formula for the sum of an infinite geometric series is S = a/(1-r), where a is the first term and r is the common ratio. Applying this formula to Achilles' race:

This calculation shows that Achilles does catch the tortoise after traveling approximately 111.11 meters. The time it takes can be calculated as distance divided by speed: 111.11 meters ÷ 10 meters/second = 11.11 seconds. In this time, the tortoise travels 11.11 meters, which added to its 100-meter head start gives 111.11 meters—the same distance Achilles traveled.

The resolution of the paradox lies in understanding that an infinite sequence of tasks can be completed in finite time. This concept was not rigorously developed until the invention of calculus and the theory of limits in the 17th and 19th centuries. The key insight is that the time intervals between successive steps become progressively smaller, approaching zero, and their sum converges to a finite value.

Mathematically, the time intervals form the sequence: 10 + 1 + 1/10 + 1/100 + … This is also a geometric series with a = 10 and r = 1/10. Its sum is:

This mathematical resolution shows that Achilles can complete the infinite sequence of tasks in finite time, thus overtaking the tortoise. The paradox arises from the intuitive but incorrect assumption that an infinite number of tasks must take infinite time.

The philosophical implications of the paradox extend beyond the mathematical resolution. It raises questions about the nature of space and time: are they continuous or discrete? If space and time are continuous, as classical physics assumes, then the infinite divisibility that leads to Zeno’s paradoxes is a real feature of the physical world. If they are discrete, as some modern quantum theories suggest, then there might be a smallest possible unit of space and time, which would resolve the paradoxes differently.

In quantum mechanics, the Planck length (approximately 1.6 × 10⁻³⁵ meters) and Planck time (approximately 5.4 × 10⁻⁴⁴ seconds) represent scales at which the classical concepts of space and time may break down. If there is a fundamental granularity to spacetime, then Zeno’s infinite subdivisions might not be physically realizable, providing a physical resolution to the paradox.

The mathematical tools developed to resolve Zeno’s paradoxes have far-reaching applications beyond this specific problem. The theory of infinite series is fundamental to calculus, physics, engineering, and many other fields. The concept that infinite processes can have finite outcomes is essential for understanding everything from compound interest to radioactive decay.

Zeno’s paradox also illustrates the importance of mathematical rigor in addressing philosophical problems. The intuitive but incorrect assumption that infinite tasks require infinite time was only corrected through the development of precise mathematical concepts. This demonstrates how mathematical innovation can resolve problems that seem intractable through purely logical reasoning.

The Achilles and the Tortoise paradox remains a valuable teaching tool for introducing concepts of infinite series, limits, and the relationship between mathematical models and physical reality. It shows how careful reasoning can reveal hidden assumptions in our understanding and how mathematical innovation can resolve apparent contradictions.

The Dichotomy Paradox, also known as the Race Course Paradox, is another of Zeno’s famous challenges to the possibility of motion. This paradox argues that before reaching any destination, a traveler must first cover half the distance, then half of the remaining distance, then half of what remains, and so on indefinitely. Since this requires completing an infinite number of tasks, Zeno concluded that motion is impossible. Like the Achilles paradox, this argument seems to contradict our everyday experience while appearing logically sound.

To make the paradox concrete, consider walking from point A to point B, a distance of 1 meter. According to Zeno’s reasoning, you must first reach the halfway point (0.5 meters), then the 3/4 meter mark (halfway between 0.5 and 1), then the 7/8 meter mark (halfway between 3/4 and 1), and so on. The distances you must traverse form the sequence: 1/2, 1/4, 1/8, 1/16, … This creates an infinite sequence of steps, each of which must be completed before reaching the destination.

Mathematically, the total distance covered is the sum of this infinite geometric series: 1/2 + 1/4 + 1/8 + 1/16 + … The first term a = 1/2 and the common ratio r = 1/2. Using the formula for the sum of an infinite geometric series S = a/(1-r):

This mathematical result shows that the infinite sequence of steps does indeed sum to the finite distance of 1 meter. The paradox arises from conflating the infinity of steps with the finiteness of the result. Modern mathematics demonstrates that an infinite process can have a finite outcome.

The time aspect of the Dichotomy Paradox is equally important. If we assume constant speed, the time taken for each step also forms a geometric series. For a speed of 1 meter per second, the times are: 1/2 second, 1/4 second, 1/8 second, 1/16 second, … This series also converges, with sum:

This calculation shows that the infinite sequence of temporal steps takes exactly 1 second to complete, matching our intuitive expectation. The paradox dissolves when we recognize that both the spatial and temporal infinite sequences converge to finite values.

The mathematical concept of limits is crucial to resolving the Dichotomy Paradox. In modern analysis, we say that the sequence of partial sums S₁ = 1/2, S₂ = 3/4, S₃ = 7/8, S₄ = 15/16, … approaches 1 as a limit. We write this as lim(n→∞) Sₙ = 1. This formal definition of limits provides the rigorous foundation that resolves Zeno’s paradoxes while preserving our intuitive understanding of motion.

The Dichotomy Paradox also raises deeper questions about the nature of space and time. If space is continuous, as classical physics assumes, then any finite interval contains infinitely many points. This infinite divisibility is what allows Zeno’s argument to generate an infinite sequence of steps. However, the mathematical theory of infinite series shows that this infinite divisibility does not prevent the completion of motion.

In modern physics, the question of whether space and time are continuous or discrete remains open. Some quantum gravity theories suggest that spacetime might have a discrete structure at the Planck scale, with a smallest possible unit of length and time. If true, this would provide a different resolution to Zeno’s paradoxes by preventing the infinite subdivisions that generate the paradoxes.

The Dichotomy Paradox has practical applications in computer science and engineering. In digital signal processing, continuous signals are approximated by discrete samples, and the theory of infinite series helps determine how many samples are needed for accurate representation. In numerical analysis, continuous processes are approximated by finite algorithms, and understanding convergence is essential for ensuring accuracy.

The paradox also illustrates the difference between potential and actual infinity. The sequence of steps in the Dichotomy Paradox represents a potential infinity—there is no last step, but each individual step is finite. The completion of the motion represents an actual infinity—the infinite sequence has been completed. The mathematical resolution shows that actual infinities can be meaningfully handled within rigorous mathematical frameworks.

Zeno’s Dichotomy Paradox has influenced the development of mathematical thinking about convergence, series, and the continuum. It forced mathematicians to develop precise definitions of infinite processes and to distinguish between different types of infinity. These developments were essential for the creation of calculus and mathematical analysis.

The paradox continues to be relevant in modern discussions of physics and philosophy. It raises questions about the relationship between mathematical models and physical reality, the nature of continuity and discreteness, and the foundations of calculus that remain active areas of research. The Dichotomy Paradox reminds us that our intuitive understanding of fundamental concepts can be misleading and that rigorous mathematical analysis is often necessary to resolve apparent contradictions.

The resolution of Zeno’s paradoxes required the development of mathematical tools that wouldn’t be invented until nearly two millennia after Zeno formulated his arguments. The concept of limits, developed as part of calculus in the 17th century and rigorously formalized in the 19th century, provides the mathematical framework that resolves the apparent contradictions in Zeno’s paradoxes. This resolution demonstrates how mathematical innovation can address philosophical problems that seem intractable through purely logical reasoning.

The fundamental insight that resolves Zeno’s paradoxes is that infinite processes can converge to finite limits. In the Dichotomy Paradox, the infinite series 1/2 + 1/4 + 1/8 + 1/16 + … converges to 1. In the Achilles and the Tortoise paradox, the infinite series representing the distances or times converges to a finite sum. The mathematical theory of infinite series shows that adding infinitely many terms can produce a finite result, resolving the core contradiction in Zeno’s arguments.

The rigorous definition of a limit is essential to this resolution. We say that a sequence a₁, a₂, a₃, … approaches a limit L if, for any positive number ε (epsilon), there exists a positive integer N such that for all n > N, |aₙ – L| < ε. This formal definition captures the intuitive idea that the terms of the sequence get arbitrarily close to L as n increases without bound.

For the partial sums of the Dichotomy Paradox, S₁ = 1/2, S₂ = 3/4, S₃ = 7/8, S₄ = 15/16, …, we can write the general term as Sₙ = 1 – 1/2ⁿ. To show that lim(n→∞) Sₙ = 1, we need to show that for any ε > 0, there exists N such that for all n > N, |(1 – 1/2ⁿ) – 1| < ε. This simplifies to 1/2ⁿ < ε, which is satisfied when n > log₂(1/ε). This rigorous proof confirms that the infinite sequence of steps sums to the finite distance.

The development of calculus by Newton and Leibniz in the 17th century provided the mathematical tools needed to handle infinite processes systematically. The derivative, which represents instantaneous rate of change, and the integral, which represents accumulation over continuous domains, both rely on the concept of limits. These tools showed that Zeno’s arguments, while logically structured, were based on an incomplete understanding of infinite processes.

In the 19th century, mathematicians like Augustin-Louis Cauchy, Karl Weierstrass, and Richard Dedekind provided rigorous foundations for calculus by formalizing the concept of limits and the real number system. This work resolved many of the logical issues that had plagued earlier treatments of infinite series and calculus, providing a solid mathematical basis for the resolution of Zeno’s paradoxes.

The ε-δ definition of limits, developed by Weierstrass, provides the precise mathematical language needed to discuss convergence rigorously. For a function f(x), we say lim(x→a) f(x) = L if for every ε > 0, there exists a δ > 0 such that 0 < |x - a| < δ implies |f(x) - L| < ε. This definition allows mathematicians to prove convergence theorems with complete logical rigor.

The mathematical resolution also requires a proper understanding of the real number system. The completeness property of real numbers—the fact that every bounded set of real numbers has a least upper bound—ensures that convergent sequences have limits within the real numbers. This property is essential for the convergence theorems that resolve Zeno’s paradoxes.

Measure theory, developed in the late 19th and early 20th centuries, provides another perspective on the resolution. In measure theory, sets of measure zero (like the individual points in Zeno’s sequences) can be “ignored” when calculating integrals or considering continuous processes. This mathematical framework shows that the infinite sequence of points in Zeno’s paradoxes has no effect on the overall motion.

The resolution of Zeno’s paradoxes also involves understanding different types of infinity. The sequence of steps in the paradoxes represents a countable infinity—there is a first step, second step, third step, and so on. The mathematical theory of infinite sets, developed by Georg Cantor, shows that countable infinities can be “completed” in ways that resolve Zeno’s concerns about infinite tasks.

Modern non-standard analysis, developed by Abraham Robinson in the 1960s, provides yet another approach to resolving Zeno’s paradoxes. This mathematical framework extends the real numbers to include infinitesimal and infinite quantities, allowing for rigorous treatment of infinitely small and infinitely large quantities. In this system, the infinite sequences in Zeno’s paradoxes can be treated as genuine mathematical objects.

The resolution of Zeno’s paradoxes has had profound implications for mathematics and science. It demonstrated that intuitive reasoning about infinity could be misleading and that rigorous mathematical analysis was necessary for understanding continuous processes. This insight influenced the development of mathematical physics, where continuous models are essential for describing everything from planetary motion to electromagnetic fields.

The mathematical tools developed to resolve Zeno’s paradoxes have applications throughout science and engineering. The theory of infinite series is used in signal processing, quantum mechanics, and numerical analysis. The concept of limits is fundamental to differential equations, which model everything from population dynamics to fluid flow. The rigorous treatment of infinity is essential for understanding fractals, chaos theory, and modern cosmology.

The resolution of Zeno’s paradoxes also illustrates the relationship between mathematical models and physical reality. While mathematical analysis shows that the paradoxes don’t prevent motion, it doesn’t directly address whether physical space and time have the continuous structure assumed by the mathematical models. This question remains active in modern physics, particularly in quantum gravity research.

Finally, the resolution of Zeno’s paradoxes demonstrates the cumulative nature of mathematical knowledge. It took over two thousand years and the contributions of many brilliant mathematicians to develop the tools needed to address Zeno’s challenges. This historical development shows how mathematical innovation builds on previous work and how seemingly abstract mathematical concepts can resolve concrete philosophical problems.